<stdio.han>

[문제 링크]

https://www.acmicpc.net/problem/1932

[난이도]

- Silver 1 

[알고리즘]

- DP

[코드]

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());
        int[][] triangle = new int[n][]; // 2차원은 가변적으로 선언
        int[][] dp = new int[n][]; // 2차원은 가변적으로 선언

        for (int i = 0; i < n; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            triangle[i] = new int[i + 1];
            dp[i] = new int[i + 1];
            for (int j = 0; j <= i; j++) {
                triangle[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        // 초기값 설정
        dp[0][0] = triangle[0][0];

        // dp 배열 채우기
        for (int i = 1; i < n; i++) {
            for (int j = 0; j <= i; j++) {
                if (j == 0) { //
                    dp[i][j] = dp[i - 1][j] + triangle[i][j];
                } else if (j == i) {
                    dp[i][j] = dp[i - 1][j - 1] + triangle[i][j];
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j - 1], dp[i - 1][j]) + triangle[i][j];
                }
            }
        }

        // dp배열의 마지막 열중 최대값 출력
        int maxSum = 0;
        for (int j = 0; j < n; j++) {
            maxSum = Math.max(maxSum, dp[n - 1][j]);
        }

        System.out.println(maxSum);
    }
}

[풀이]

dp 2차원 배열은 정사각형일 필요가 없으므로 입력받을 때 마다 2차원배열의 2차원의 크기를 i+1 로 초기화 해준다.

        int[][] triangle = new int[n][]; // 2차원은 가변적으로 선언
        int[][] dp = new int[n][]; // 2차원은 가변적으로 선언

        for (int i = 0; i < n; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            triangle[i] = new int[i + 1];
            dp[i] = new int[i + 1];
            for (int j = 0; j <= i; j++) {
                triangle[i][j] = Integer.parseInt(st.nextToken());
            }
        }

dp배열의 점화식은 아래와 같다.

dp[i][j] = Math.max(dp[i - 1][j - 1], dp[i - 1][j]) + triangle[i][j];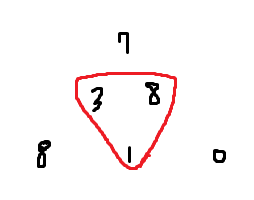

dp[i][j] 는 dp[i-1][j-1]와 dp[i-1][j] 두 수를 비교해 둘중 큰 값을 선택한다. 하지만 여기서 문제가있다.

삼각형중 가장 왼쪽의 수와 가장 오른쪽의 수는 두 수를 비교할 수가 없다.

가장 왼쪽의 수는 비교할 수가 하나밖에없어 무조건 dp[i-1][j]를 선택해야만 한다. 그래서 따로 조건문을 만들어준다.

		if (j == 0) { //
                    dp[i][j] = dp[i - 1][j] + triangle[i][j];
                }

삼각형의 가장 오른쪽의 수도 비교할 수가 하나밖에 없기때문에 무조건 dp[i-1][j-1]를 선택해야만 한다.

		else if (j == i) {
                    dp[i][j] = dp[i - 1][j - 1] + triangle[i][j];
                }

[문제 링크]

https://www.acmicpc.net/problem/11055

[난이도]

- Silver 2

[알고리즘]

- DP

[코드]

import java.io.*;
import java.util.*;

public class Main {
    static int[][][] dp = new int[51][51][51];
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));


        int N = Integer.parseInt(br.readLine());
        int[] arr = new int[N];


        StringTokenizer st = new StringTokenizer(br.readLine());
        for (int i = 0; i < N; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
        }

        int[] dp = new int[N];
        for (int i = 0; i < N; i++) {
            dp[i] = arr[i];
            for (int j = 0; j < i; j++) {
                if (arr[j] < arr[i]) {
                    dp[i] = Math.max(dp[i], dp[j] + arr[i]);
                }
            }
        }
        int answer = 0;
        for (int i = 0; i < N; i++) {
            answer = Math.max(answer, dp[i]);
        }
        System.out.println(answer);
    }
}

[풀이]

LIS 알고리즘을 활용한 문제이다.

if (arr[j] < arr[i]) {
                    dp[i] = Math.max(dp[i], dp[j] + arr[i]);
                }

dp[n] 은 arr[n]이 가장 큰 수인 증가하는 부분 수열일 때 증가하는 부분 수열의 합이다.

[문제 링크]

https://www.acmicpc.net/problem/9184

[난이도]

- Silver 2

[알고리즘]

- DP

[코드]

import java.io.*;
import java.util.*;

public class Main {
    static int[][][] dp = new int[51][51][51];
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st;

        while (true) {
            st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            int c = Integer.parseInt(st.nextToken());

            if (a == -1 && b == -1 && c == -1) {
                break;
            }

            bw.write("w(" + a + ", " + b + ", " + c + ") = " + w(a, b, c) + "\n");
        }
        bw.flush();
        bw.close();
        br.close();
    }

    static int w(int a, int b, int c) {
        if (a <= 0 || b <= 0 || c <= 0) {
            return 1;
        } else if (a > 20 || b > 20 || c > 20) {
            return w(20, 20, 20);
        } else if (dp[a][b][c] != 0) {
            return dp[a][b][c];
        } else if (a < b && b < c) {
            dp[a][b][c] =  w(a, b, c - 1) + w(a, b - 1, c - 1) - w(a, b - 1, c);
        } else {
            dp[a][b][c] = w(a - 1, b, c) + w(a - 1, b - 1, c) + w(a - 1, b, c - 1) - w(a - 1, b - 1, c - 1);
        }
        return dp[a][b][c];
    }
}

[풀이]

점화식은 이미 나와있기 때문에 고민할 필요는 없다. 다만 그대로 사용하면 시간초과가 발생한다. 이를 해결하기 위해

메모이제이션을 활용해야 한다. 함수는 다음과 같이 작성했다.

static int w(int a, int b, int c) {
        if (a <= 0 || b <= 0 || c <= 0) {
            return 1;
        } else if (a > 20 || b > 20 || c > 20) {
            return w(20, 20, 20);
        } else if (dp[a][b][c] != 0) {
            return dp[a][b][c];
        } else if (a < b && b < c) {
            dp[a][b][c] =  w(a, b, c - 1) + w(a, b - 1, c - 1) - w(a, b - 1, c);
        } else {
            dp[a][b][c] = w(a - 1, b, c) + w(a - 1, b - 1, c) + w(a - 1, b, c - 1) - w(a - 1, b - 1, c - 1);
        }
        return dp[a][b][c];
    }

아래 조건문을 활용하면 이미 한번 계산한 값이라면 저장해놓은 배열에서 꺼내서 사용할 수 있기 때문에 시간을 효율적으로 줄일 수 있다.

	else if (dp[a][b][c] != 0) {
            return dp[a][b][c];
        }

아래 조건문을 활용해 계산한 값을 dp 배열에 저장해 나중에 사용할 수 있다.

	else if (a < b && b < c) {
            dp[a][b][c] =  w(a, b, c - 1) + w(a, b - 1, c - 1) - w(a, b - 1, c);
        } else {
            dp[a][b][c] = w(a - 1, b, c) + w(a - 1, b - 1, c) + w(a - 1, b, c - 1) - w(a - 1, b - 1, c - 1);
        }

[문제 링크]

https://www.acmicpc.net/problem/1965

[난이도]

- Silver 3

[알고리즘]

- DP

[코드]

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());
        int[] arr = new int[n];
        int[] dp = new int[n];

        StringTokenizer st = new StringTokenizer(br.readLine(), " ");
        for (int i = 0; i < n; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
        }

        // DP 배열 초기화
        Arrays.fill(dp, 1);

        int max = 0;

        // LIS 알고리즘 적용
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < i; j++) {
                if (arr[j] < arr[i]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            max = Math.max(max, dp[i]);
        }

        // 결과 출력
        System.out.println(max);
    }
}

[풀이]

dp[n] = n번째 상자를 마지막으로 포함하는 가장 긴 부분수열

[문제 링크]

https://www.acmicpc.net/problem/8394

[난이도]

- Silver 3

[알고리즘]

- DP

[코드]

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());
        long[] dp = new long[n + 1];

        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = (dp[i - 2] + dp[i - 1]) % 10;
        }
        System.out.println(dp[n]);


        /**
         * dp[1] = 1
         * dp[2] = 2
         * dp[3] = 3
         * dp[4] = 5
         * dp[5] = 8
         * 피보나치 수열임
         */

    }
}

[풀이]

피보나치 수열의 마지막 자리 숫자만 출력하는 문제이다. 수를 10으로 나눈 나머지의 값이 마지막 숫자이다.