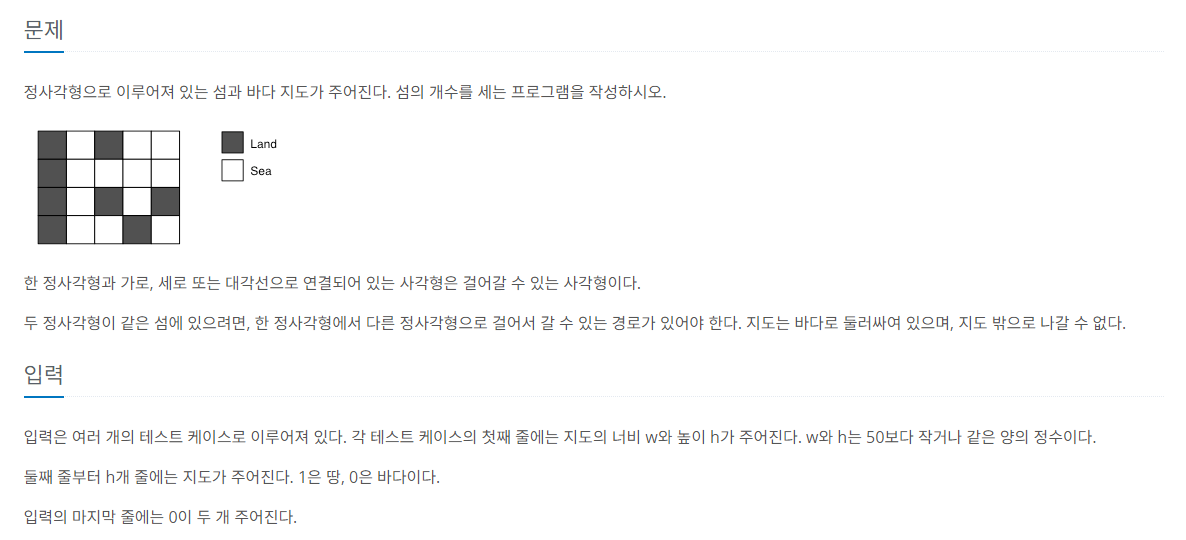
백준 4963번: 섬의 개수[JAVA]
https://www.acmicpc.net/problem/11724
11724번: 연결 요소의 개수
첫째 줄에 정점의 개수 N과 간선의 개수 M이 주어진다. (1 ≤ N ≤ 1,000, 0 ≤ M ≤ N×(N-1)/2) 둘째 줄부터 M개의 줄에 간선의 양 끝점 u와 v가 주어진다. (1 ≤ u, v ≤ N, u ≠ v) 같은 간선은 한 번만 주어
www.acmicpc.net


[정답 코드]
import java.io.*;
import java.util.*;
public class Main {
static int N; // 정점의 개수
static int M; // 간선의 개수
static int[][] graph; // 그래프배열
static boolean[] visited; //방문한 자리
static int count = 0; // 연결요소의 개수
public static void main(String[] args) throws Exception {
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
graph = new int[N][N];
visited = new boolean[N];
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine(), " ");
int u = Integer.parseInt(st.nextToken()) - 1; // 편하게 하기위해 -1
int v = Integer.parseInt(st.nextToken()) - 1;
graph[u][v] = 1;
graph[v][u] = 1;
}
for (int i = 0; i < N; i++) {
if (!visited[i]) { //방문하지 않은 자리라면 bfs함수 실행 후 count++;
bfs(i);
count++;
}
}
System.out.println(count);
}
public static void bfs(int start) {
Queue<Integer> q = new LinkedList<>(); // 큐 선언
q.offer(start); //큐에 삽입
visited[start] = true; //방문한곳 표시
// 해당 기준으로 연결된 지점을 확인
while (!q.isEmpty()) {
int tmp = q.poll();
for (int i = 0; i < N; i++) {
if (graph[tmp][i] == 1 && !visited[i]) {
q.offer(i);
visited[i] = true;
}
}
}
}
}
[설명]
bfs 문제로 방향없는 그래프를 그린 후 조건에 해당하는 노드를 만나면 bfs 함수를 실행해 인접노드를 찾는다. 방문한 노드는 true 로 만들며 인접한노드이며 방문하지 않은 노드를 계속 찾는다. 탐색이 끝나면 count 를 1 증가시킨다. N번 노드 까지 탐색이 끝나면 출력한다.
'코딩테스트' 카테고리의 다른 글
| 백준 9663번: N-Queen[JAVA] (0) | 2023.11.10 |
|---|---|
| 백준 7576번: 토마토[JAVA] (1) | 2023.11.03 |
| 백준 4963번: 섬의 개수[JAVA] (1) | 2023.11.03 |
| 백준 14888번: 연산자 끼워넣기[JAVA] (1) | 2023.10.27 |
| 백준 1914번: 하노이 탑[JAVA] (1) | 2023.10.27 |