<stdio.han>

다익스트라 알고리즘(Dijkstra's algorithm)

다익스트라 혹은 데이크스트라 알고리즘 이라고부르는 이것은 도로 교통망 같은 곳에서 나타날 수 있는 그래프에서 꼭짓점 간의 최단경로를 찾는 알고리즘이다.

일반적인 다익스트라 알고리즘문제로는 한 꼭짓점을 "소스" 꼭짓점으로 고정하고 그래프의 다른 모든 꼭짓점까지의 최단경로를 찾는 알고리즘으로 최단 경로 트리를 만드는것이다. 그래프의 간선마다 가중치가 존재하고, 음의 가중치는 존재하지 않는다. 음의 가중치가 존재한다면 다익스트라를 사용할 수 없다.

구현하는 방법에는 인접행렬방식과 우선순위 큐 두가지가 있다. 먼저 다익스트라를 이해하기 위해 인정행렬이 더 간단하기 때문에 먼저 알아보자.

동작 과정을 간단하게 설명하자면 다음과 같다.

1. 출발 노드를 설정한다.

2. 출발노드에서 이웃한 노드중 거리가 가장 짧은순으로 선택해 가중치를  각 노드에 기록한다.

3. 기록한 노드중 거리가 가장 짧은 노드를 선택후 다시 방문하지 않은 이웃 노드를 탐색한다.

4. 재탐색하는 노드에는 기록된 가중치 + 간선 가중치와 기록되어있는 가중치중 작은 것을 기록한다.

5. 위 과정을 반복한다.

[예시]

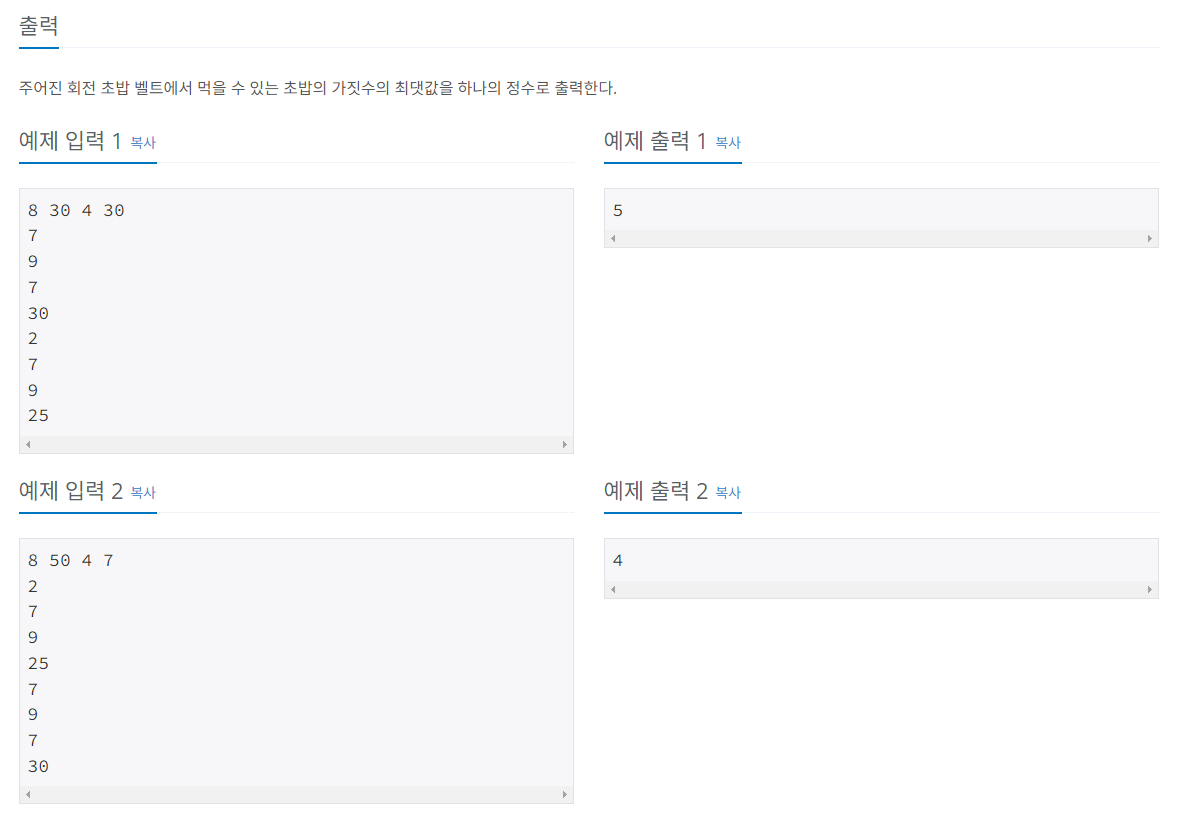
먼저 위 그림을 예로 이차원 배열을 활용해 구현해보자. 

가중치를 가중치 인접 행렬(2차원 배열)에 저장한다. 연결되지 않은 노드는 INF를 기록한다.

시작 노드인 1번 노드기준의 각 노드의 가중치를 기록한 배열이다.

인정합 노드인 2, 3, 6번 노드순으로 탐색해 나가면 값을 수정해보자. 먼저 가장 짧은 노드인 2번노드를 먼저 탐색해보자

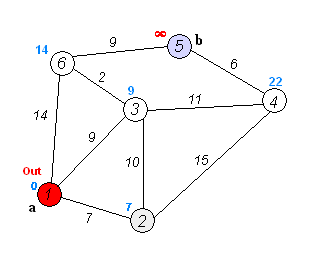
2번노드

2번의 인접노드중 방문하지 않은 노드인 3번 과 4번 노드를 보자

먼저 3번 노드를 보면 2번노드의 가중치(7) + 간선의 가중치(10) = 17

3번 노드의 가중치 = 9

최솟값을 찾는 것이기 때문에 3번 노드의 가중치는 그대로 9이다.

4번 노드는 INF 였지만 2번노드의 가중치(7) +간선의 가중치(15) = 22가 되어 4번 노드의 가중치는 22가 기록된다.

탐색이 끝났다면 1번의 인접노드 2, 3, 6 중 그 다음 노드인 3번 노드로 넘어간다.

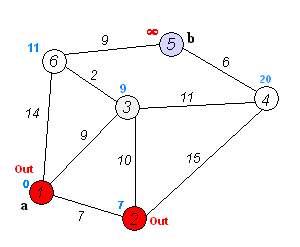
3번 노드

3번노드의 인접노드중 방문 하지 않은 노드 4번 노드, 6번 노드를 보자

3번 노드의 가중치(9) + 간선의 가중치(11) = 20

3번 노드의 가중치(9) + 간선의 가중치(2) = 11

그다음 노드 6번 노드를 탐색해보자

6번 노드

6번노드의 인접노드중 방문하지 않은 노드인 4번 노드를 보자

6번 노드의 가중치(11) + 간선의 가중치(9) = 20

원래 5번의 가중치는 INF 였기때문에 더 짧은 가중치인 20으로 수정된다.

마지막 방문하지 않은 노드인 4번 노드를 확인해보자

4번 노드

4번노드에서 방문하지 않은 인접노드 5번노드까지를 보면

4번 노드의 가중치(20) + 간선의 가중치(6) = 26 이므로

값을 수정하지 않고 원래의 가중치인 20으로 남겨둔다.

5번 노드는 인접한 모든 노드가 방문을 완료한 노드기 때문이 탐색을 종료한다.

최종적인 가중치 기록 배열을 보자

1번 노드 -> 1번 노드 : 0

1번 노드 -> 2번 노드 : 7

1번 노드 -> 3번 노드 : 9

1번 노드 -> 4번 노드 : 20

1번 노드 -> 5번 노드 : 20

1번 노드 -> 6번 노드 : 11

[시간복잡도]

기본적인 다익스트라의 시간복잡도는 

V : 노드의 숫자, E : 간선의 숫자 라고 볼때 O(V^2) 이다.

하지만 우선순위 큐등을 사용해 이를 좀더 개선하면 O((V + E)logV) 가 나온다.

이 인접행렬방식을 자바 코드로 구현하자면 다음과 같다.

[코드]

import java.io.*;
import java.util.*;

public class Main {

    static int INF = Integer.MAX_VALUE;
    static int N, E; // 노드의 개수, 간선의 개수
    static int[][] Graph; // 노드들간의 가중치를 저장할 변수
    static int[] Dist; // 최단 거리를 저장할 변수
    static boolean[] Check; // 해당 노드를 방문했는지 체크할 변수
    public static void main(String[] args) throws Exception {
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine(), " ");

        N = Integer.parseInt(st.nextToken()); // 노드의 개수
        E = Integer.parseInt(st.nextToken()); // 간선의 개수
        Graph = new int[N][N];
        Dist = new int[N];

        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                // 인접행렬 모든 값 INF 로 초기화
                Graph[i][j] = INF;
            }
        }

        for (int i = 0; i < E; i++) {
            st = new StringTokenizer(br.readLine(), " ");
            int u = Integer.parseInt(st.nextToken());
            int v = Integer.parseInt(st.nextToken());
            int cost = Integer.parseInt(st.nextToken());
            Graph[u][v] = Graph[v][u] = cost; // 양방향 간선
        }

        dijkstra(0);

        bw.flush();
        bw.close();
        br.close();
    }

    public static void dijkstra(int v) {
        Dist = new int[N];
        Check = new boolean[N];

        // Dist 값 초기화
        for (int i = 0; i < N; i++) {
            Dist[i] = INF;
        }

        // 시작노드값 초기화
        Dist[v] = 0;
        Check[v] = true;

        // 결과값 출력
        for (int i = 0; i < N; i++) {
            if(Dist[i] == INF) System.out.print("INF" + "\t");
            else System.out.print(Dist[i]+"\t");
        }
        System.out.println("");

        // 인접한 노드 Dist 갱신
        for (int i = 0; i < N; i++) {
            if (!Check[i] && Graph[v][i] != INF) { // 방문하지 않은 노드 && INF가 아닌경우
                Dist[i] = Graph[v][i]; //값 갱신
            }
        }

        // 결과값 출력
        for (int i = 0; i < N; i++) {
            if(Dist[i] == INF) System.out.print("INF" + "\t");
            else System.out.print(Dist[i]+"\t");
        }
        System.out.println("");

        for (int i = 0; i < N - 1; i++) {
            // 모든 노드가 true가 될때까지 해야하지만
            // 노드가 N개라면 다익스트라를 위해 반복수는 N-1 번만 하면 됨.
            int min = Integer.MAX_VALUE;
            int min_index = -1;

            // 노드 최소값 찾기
            for (int j = 0; j < N; j++) {
                if (!Check[j]) { //방문하지 않은 노드
                    if (Dist[j] < min) { // 방문하지 않은 노드중 가중치가 가장 작은 노드를 찾는다.
                        min = Dist[j];
                        min_index = j; // 가중치가 가장 작은 노드의 번호를 저장
                    }
                }
            }

            // 다른 노드를 거쳐 가는 것이 더 비용이 적은지 확인
            Check[min_index] = true; // 방문한 노드 true
            for (int j = 0; j < N; j++) {
                if (!Check[j] && Graph[min_index][j] != INF) {
                    if (Dist[min_index] + Graph[min_index][j] < Dist[j]) {
                        Dist[j] = Dist[min_index] + Graph[min_index][j];
                    }
                }
            }

            // 결과값 출력
            for (int j = 0; j < N; j++) {
                if(Dist[j] == INF) System.out.print("INF" + "\t");
                else System.out.print(Dist[j]+"\t");
            }
            System.out.println("");
        }
    }
}

[결과]

첫째줄에 노드와 간선의 수를 입력받고 그다음줄 부터 시작노드, 도착노드, 가중치 를 입력해준다.

편리하게 구현하기 위해 문제에서는 가장 작은 노드가 1번노드지만 구현할때는 0번노드로했다.

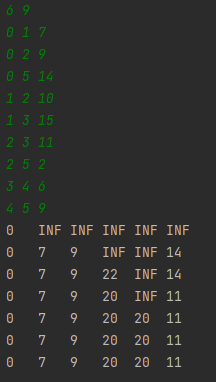
결과 값을 보면 예시에서 보여준 가중치 배열과 같은 결과값을 보여준다.

백준 14888번: 연산자 끼워넣기[JAVA]

https://www.acmicpc.net/problem/14888

[정답 코드]

import java.io.*;
import java.math.BigInteger;
import java.util.*;

public class Main {
    static int MAX = Integer.MIN_VALUE;
    static int MIN = Integer.MAX_VALUE;
    static int N; // 숫자 개수
    static int[] arr; // 숫자 배열
    static int[] op = new int[4]; // 연산자 배열
    public static void main(String[] args) throws Exception {
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine(), " ");

        // 숫자 갯수 입력
        N = Integer.parseInt(st.nextToken());

        // 숫자 배열 입력
        arr = new int[N];
        st = new StringTokenizer(br.readLine(), " ");
        for (int i = 0; i < N; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
        }

        // 연산자 갯수 입력
        st = new StringTokenizer(br.readLine(), " ");
        for (int i = 0; i < 4; i++) {
            op[i] = Integer.parseInt(st.nextToken());
        }

        backTracking(arr[0], 1);

        //최대값 최소값 출력
        bw.write(MAX + "\n" + MIN);

        bw.flush();
        bw.close();
        br.close();
    }

    // 로직
    public static void backTracking(int num, int idx) {

        // idx == N 이 되면 종료, arr 끝까지 탐색했다는 의미
        if (idx == N) {
            MAX = Math.max(MAX, num);
            MIN = Math.min(MIN, num);
            return;
        }

        for (int i = 0; i < 4; i++) {
            // 해당 연산자가 존재하면, 해당연산자 사용한 후 개수 하나 제거
            if (op[i] > 0) {
                op[i]--;
                switch (i) {
                    case 0:	backTracking(num + arr[idx], idx + 1);	break;
                    case 1:	backTracking(num - arr[idx], idx + 1);	break;
                    case 2:	backTracking(num * arr[idx], idx + 1);	break;
                    case 3:	backTracking(num / arr[idx], idx + 1);	break;
                }
                // 재귀호출이 종료되면 다시 해당 연산자 개수를 복구한다.
                op[i]++;
            }
        }
    }
}

[정리]

그림의 예가 약간 잘못된것같고 이상하지만 참고하고 보자. 그림을 예로 들어보자면 입력값이 첫째 줄에 3, 둘째 줄에 2 3 4 셋째 줄에 1 1 1 1을 입력받았을 경우의 대략적인 그림이다. 첫번째 숫자부터시작해 2 + 3 - 4 순서대로 계산을 하고 그 다음은 2 + 3 * 4, 그 다음은 2 + 3 / 4 순서대로 진행하게 된다. 숫자가 더 많거나 연산자가 더 많을 경우에도 그림과 같이 진행된다고 보면 된다.

[느낀점]

아직 하노이 알고리즘도 그렇고, dfs, bfs 등 어려운 알고리즘은 혼자만의 생각으로는 아직 풀 수 없는것같다. 다른 글을 참고해가며 정말 어려울 경우에는 클론코딩을 해가며 풀게된다. 중요한 점은 그냥 참고하고 끝나는게 아니라 문제를 풀 때 만큼은 그림으로 그려가며 완벽하게 이해하는게 중요한것 같다.

백준 1914번: 하노이 탑[JAVA]

https://www.acmicpc.net/problem/1914

[정답 코드]

import java.io.*;
import java.math.BigInteger;
import java.util.*;

public class Main {
    static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static int N = 0;

    public static void main(String[] args) throws Exception {

        // 원판의 개수 입력
        N = Integer.parseInt(br.readLine());

        //관계식
        System.out.println(BigInteger.TWO.pow(N).subtract(BigInteger.ONE));

        // N이 20 이하일 경우 과정 출력
        if (N <= 20) {
            hanoi(N, 1, 2, 3);
        }

        bw.flush();
        bw.close();
        br.close();
    }

    // [로직] n 옮길 원판, from 시작 기둥, tmp 거쳐갈 기둥, to 도착 기둥
    public static void hanoi(int n, int from, int tmp, int to) throws IOException{

        // n == 1 일경우 바로 이동
        if (n == 1) {
            bw.write(from + " " + to + "\n"); // 이동
            return;
        }

        hanoi(n - 1, from, to, tmp);
        bw.write(from + " " + to + "\n"); // 이동

        hanoi(n-1, tmp, from, to);
    }
}

[시행착오]

그림판으로 그림까지 그려가며 하노이 탑을 공부하고 이해하려 노력했다. 코드는 다른글을 참고했지만 이해하기는했다.

처음엔 메모리초과가 발생했다. 알아본 결과 수가 너무 커질 경우 메모리 초과가 발생해 count 를 int 에서 long 으로 변경했다. 그런데 이번엔 시간초과가 발생했다. long 도 문제였다. 한 번 움직일 때마다 count 를 1씩 늘려주는 방식은 N이 매우 큰수가 될때 시간을 많이 잡아먹어 효율이 안좋았다. 애초에 시작할때 움직일만큼의 방정식을 계산해 출력을 해주는것이좋다. 그리고 그때의 타입은 BigInteger가 되어야만 했다. int, long 둘다 N이 100일 경우 메모리를 초과하기 때문이다.

N 이 20이상일 경우에는 hanoi() 자체가 실행되는순간 시간과 메모리를 많이 차지하기때문에 20 이하일 경우에만 hanoi()를 실행하게했다.

[정리]

원판의 개수 N을 입력받는다.

그 N을 이용해 관계식을 도출해 원판이 움직이는 횟수를 출력한다.

N이 20 이하일 경우 hanoi()를 실행한다.

[하노이 알고리즘]

그림과 hanoi() 를 같이 보면 이해하기 쉽다.

N개의 원판이 1번기둥에 있다. 제일 아래 큰 원판이 N 번째 원판이다.

hanoi(N, from, tmp, to) 실행

1단계 : N번째 원판을 옮기기 위해서는 N번째 원판을 제외한 N-1 번째부터 1번째 원판까지를 2번 기둥으로 옮긴다.

hanoi(N-1, from, to, tmp)

2단계 : N번째 원판을 3번 기둥으로 옮긴다.

이동

3단계 : N-1 번째부터 1번째 원판을 3번기둥으로 옮긴다.

hanoi(N-1, tmp, from, to)

이렇게 간단하게 3단계로 구성되어있다. 직접 알고리즘을 짜려면 어렵지만 막상 알고나면 생각보다 어렵지 않다.

백준 17609번: 회문[JAVA]

https://www.acmicpc.net/problem/17609

[정답 코드]

import java.util.*;
import java.io.*;

public class Main {
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine(), " ");

        // 문자열의 개수를 나타내는 정수 T
        int T = Integer.parseInt(st.nextToken());
        // 문자열을담는 배열
        String[] arr = new String[T];
        String str = "";

        //문자열 입력받은 후 배열에 저장
        for (int i = 0; i < T; i++) {
            str = br.readLine();
            System.out.println(palindrome(0, str.length()- 1, str, 0));
        }
    }

    // 로직
    private static int palindrome(int start, int end, String s, int check) {
        // 문자 삭제를 2번이상 할 경우 바로 2를 반환
        if (check >= 2) {
            return 2;
        }

        // start 포인터와 end 포인터가 만나거나 지나치기 전까지 반복
        while (start < end) {
						// 같을 경우 포인터 한칸 진행
            if (s.charAt(start) == s.charAt(end)) {
                start++;
                end--;
            } else {
                // ex) abbab 같은 경우 두 경우를 비교해 더 작은 수를 반환
                return Math.min(palindrome(start + 1, end, s, check + 1), palindrome(start, end - 1, s, check + 1));
            }
        }
        return check;
    }
}

[정리]

투 포인터 알고리즘과 재귀함수를 활용해 풀었다. 처음엔 재귀함수 없이 while 문과 for 문으로 해결하려고 했지만 반례를 발견할 때 마다 코드가 한줄 한줄 추가되더니 스파게티 코드가 되었다. 몇시간 동안 수정 후 반례 abbab 를 만났을 때 왼쪽 문자를 제거했을 경우와 오른쪽 문자를 제거했을 경우 두 가지 모두를 생각해야 한다는 걸 깨닫고 수정하려 했지만 이미 코드는 난장판이 되어있었다. 그래서 싹 다 지우고 혼자 해결하는것을 포기하고 구글링을하며 반정도 클론코딩을 하며 해결했다. 4시간 정도 걸려서 풀었지만 막상 풀고나니 처음 시작을 제대로 했더라면 금방 풀수있는 문제였다.

백준 15961번: 회전 초밥[JAVA]

https://www.acmicpc.net/problem/15961

[정답 코드]

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine()," ");

        // N=접시의 수, d=초밥의 가짓수, k=연속해서 먹는 접시의 수, c=쿠폰 번호
        int N = Integer.parseInt(st.nextToken());
        int d = Integer.parseInt(st.nextToken());
        int k = Integer.parseInt(st.nextToken());
        int c = Integer.parseInt(st.nextToken());

        // 회전 초밥 배열
        int[] dishes = new int[N];
        for(int i=0;i<N;i++){
            dishes[i] = Integer.parseInt(br.readLine());
        }

        //먹은 초밥 배열 먹으면 1, 안먹으면 0
        int[] eat = new int[d+1];

        // 0번부터 k개 먹었을 경우 상태
        int cnt = 0;
        for(int i=0;i<k;i++){
            if(eat[dishes[i]] == 0) {
                cnt++;
            }
            eat[dishes[i]]++;
        }

        // 먹을 수 있는 초밥의 가짓수의 최댓값, 기본 값은 0번부터 k개 먹었을 경우의 최대값
        int max = cnt;

        //투포인터 초기화
        int start = 1;
        int end = k;

        //로직
        while(true){
            if(eat[dishes[start-1]] == 1) { // start-1 초밥이 이미 먹은 초밥이라면 cnt--
                cnt--;
            }
            // else 아니라면 그대로
            //먹은 초밥 배열 --
            eat[dishes[start-1]]--;

            //새로운 초밥이 먹은 초밥이라면 cnt++
            if(eat[dishes[end]] == 0) {
                cnt++;
            }
            // else 아니라면 그대로
            //새로 먹은 초밥 배열 ++
            eat[dishes[end]]++;

            if(eat[c] == 0) { //쿠폰초밥을 안먹었다면 max, cnt+1 중 큰 수
                max = Math.max(max, cnt+1);
            } else { //쿠폰초밥을 이미 먹었다면 그냥 비교
                max = Math.max(max, cnt);
            }

            start++;
            end++;
            if(end==N) { //end포인터가 배열끝까지 갔을 경우 처음으로
                end = 0;
            }
            if(start==N) { //start 포인터가 배열 끝까지 갔을 경우 종료
                break;
            }
        }
        System.out.println(max);

        bw.flush();
        bw.close();
        br.close();
    }
}

[정리]

투 포인터 알고리즘을 이용해 푸는 문제이다. 시작지점과 끝지점 포인터를 만들어 창문이 움직이듯이 정해진 범위를 이동해 가며 푸는 문제이다. 슬라이딩 윈도우 알고리즘이라고도 부른다.

백준 2531번과 N의 범위를 제외하고 똑같은 문제이다. 이유는 모르겠지만 2531번 문제에서는 96%에서 실패가 나온다...